polardetective

Let Q be an arithmetic expression written in infix notation. Besides operands and operators, Q may also contain left and right parentheses. Iconcool Customer Data Manager 2.2 Build 10302. We assume that the operators in Q c onsist only of exponentiations (↑), multiplications (*), divisions (/), additions (+) and subtractions (-), and that they have the usual three levels of precedence as given above. We also assume that operators on the same level, including exponentiations, are performed from left to right unless otherwise indicated by parentheses.

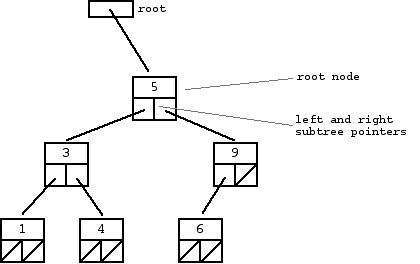
This is a C++ Program to construct an Expression tree for an Infix Expression. A binary expression tree is a specific application of a binary tree to evaluate certain. C program to construct an expression tree for a valid input arithmetic expression display the expression in infix prefix and postfix forms? Here we want to build an expression tree with this expression. The Hunger Games Team Names there. The Telnet program runs on your computer and connects your PC to a. /* C program to implement postfix expression tree and calculating its value */. Printf(' nThe value of the postfix expression you entered is%d n',ans).

(This is not standard, since expressions may contain unary operators and some languages perform the exponentiations from right to left. However, these assumptions simplify our algorithm.) The following algorithm transforms the infix expression Q into its equivalent postfix expression P. The algorithm uses a stack to temporarily hold operators and left parentheses. The postfix expression P will be constructed from left to right using the operands from Q and the operators, which are removed from STACK.

We begin by pushing a left parenthesis onto STACK and adding a right parenthesis at the end of Q. The algorithm is completed when STACK is empty. 69 Algorithm: POLISH(Q, P) Suppose Q is an arithmetic expression written in infix notation. This algorithm finds the equivalent postfix expression P. Push '(' onto STACK, and add ')' to the end of Q. Scan Q from left to right and repeat Steps 3 to 6 for each element of Q until the STACK is empty: 3. If an operand is encountered, add it to P.

If a left parenthesis is encountered, push it onto STACK. If an operator ⊗ is encountered, then: (a) Repeatedly pop from STACK and add to P each operator (on the top of STACK) which has the same precedence as or higher precedence than ⊗. (b) Add ⊗ to STACK. [End of If structure. Ithenticate Software Free Download more. ] 6. If a right parenthesis is encountered, then: (a) Repeatedly pop from STACK and add to P each operator (on the top of STACK) until a left parenthesis is encountered.